多边形序列

ID: 2790

Type: RemoteJudge

1000ms

256MiB

Difficulty: (None)

Uploaded By:

No submission language available for this problem.

题目描述

有一类特殊的多边形我们把它称为直角多边形，指的是该多边形的每一个

内角都为 90度或 270度，即每一个角都是直角。

表示一个直角多边形的一种方法是使用多边形序列，多边形序列含两种元

素：L表示 90度、R表示 270度。从直角多边形的任意一个角开始，以逆时针的

顺序对角进行顺序排列，绕一圈后所得到的序列便是多边形序列。比如正方形

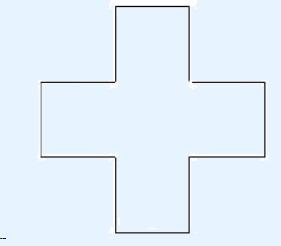
的序列为LLLL，而如下图所示的图形可表示为LLRLLRLLRLLR。显然，一个直

角多边形有多种表示序列，而一个序列也对应着多个直角多边形。

对于一个直角多边形，如果存在一个多边形内的点，使得从这个点可以看

到多边形边上的每一个点，我们认为这个直角多边形是“可观察的”。现在对于

给定的序列长度 n，请问有多少个序列长度为 n 的不同的多边形序列，满足它

所代表的所有直角多边形中，存在一个“可观察的”直角多边形。

包含一个正整数 n。

包含一个正整数，表示种数。

N<=10^100000