6 条题解
-
3
题解++
http://www.xmoj.com.cn/p/58↑题目传送门
1、阅读题目
输入一个整数n(n>=2 & n<= 45)
求出一个斐波那契数列的前n项。
2、What is 斐波那契数列?
斐波那契数列(Fibonacci sequence),又称[黄金分割]数列,因数学家莱昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义: *F (0)=0, F (1)=1, F (n)= F (n - 1)+ F (n - 2)( *n * ≥ 2, n * ∈ N)*在现代物理、准[晶体结构]、化学等领域,斐波纳契数列都有直接的应用。(form:百度百科)
3、开始头脑风暴
看到这道题,本人的第一想法就是——打表。
这道题的数据范围非常的小 没错,打表应该是这道题最最简单(没有之一)的做法了。 好哒,废话不多说,直接开打:
int a[50] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765,10946,17711,28657,46368,75025,121393,196418,317811,514229,832040, 1346269, 2178309, 3524578, 5702887,9227465,14930352,24157817,39088169,63245986,102334155,165580141,267914296,433494437,701408733,1134903170}
温馨提示:表都有了,自己上手尝试一下?
完结撒花🎉️
-
2
斐波那契数列
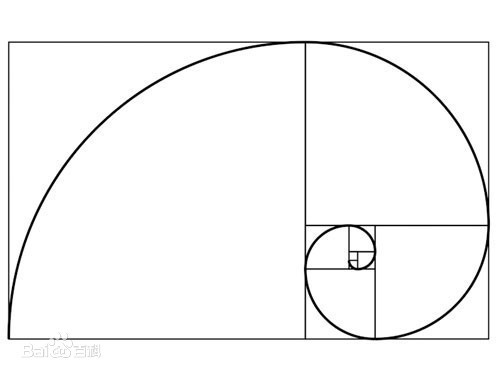 *斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义: F (0)=0, F (1)=1, F (n)= F (n - 1)+ F (n - 2)( n * ≥ 2, n * ∈ N)在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
*斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardo Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波那契数列以如下被以递推的方法定义: F (0)=0, F (1)=1, F (n)= F (n - 1)+ F (n - 2)( n * ≥ 2, n * ∈ N)在现代物理、准晶体结构、化学等领域,斐波那契数列都有直接的应用,为此,美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。using namespace std; int n[50],s,a=3,b=0,c; int main(){ cin>>s; c=s; while(c!=0){ if(s==2){ cout<<"1 1"<<endl; b=1; break; }else if(s!=2){ n[0]=1; n[2]=1; n[a]=n[a-1]+n[a-2]; a++; c--; } } if(b==0){ for(int i=2;i<=s+1;i++){ cout<<n[i]<<' '; } } return 0; } -
2
#include <bits/stdc++.h>
using namespace std;
int main(){
//菲波那契数列是指这样的数列: 数列的第一个和 第二个数都为1,接下来每个数都等于前面2个数之 和。
int n;
cin>>n;
int a[50]={1,1};//题目说n<=45我们开50个,防止 越界,将第一和第二个数赋值为1.
for(int i=2;i<=n;i++){//数组下标从0开始,我们 从下标2开始遍历,遍历到n.
a[i]=a[i-1]+a[i-2];//下标为i的为前两数之和
}
for(int i=0;i<=n-1;i++){//还是那句话,数组下标 从0开始,所以我们输出到下标n-1
cout<<a[i]<<" ";//输出 } }
-
0
#include <bits/stdc++.h> using namespace std;
int a[50] = {1,1}; int main() { int n; cin >> n; if(n>2) { cout << 1 << " " << 1 << " "; for(int i = 2;i < n;i++) { a[i] = a[i-1]+a[i-2]; cout << a[i] << " "; } } else if(n1) { cout << 1; } else if(n2) { cout << 1 << " " << 1; } return 0; }
- 1
信息
- ID
- 58
- 时间
- 1000ms
- 内存
- 256MiB
- 难度
- 5
- 标签
- 递交数
- 109
- 已通过
- 42
- 上传者
